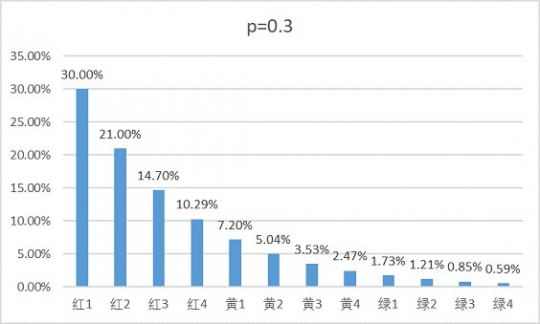
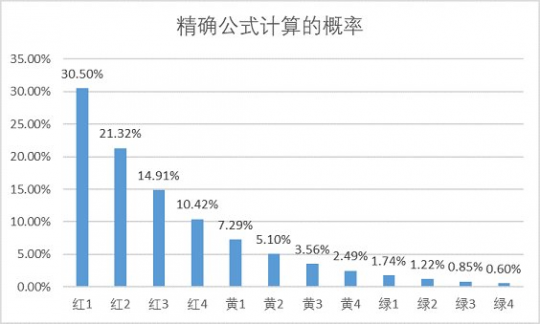
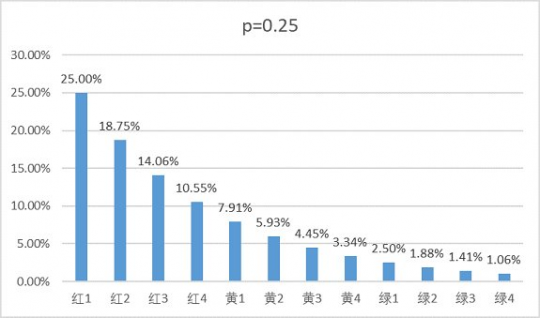
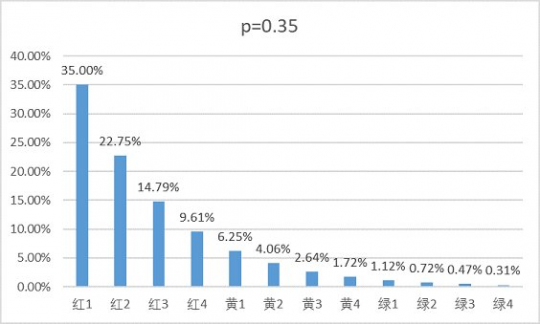
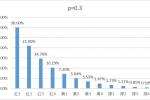
众所周知，普雷红队容易11点，绿队容易超金

虽然我一直不信这个说法，但前两天我2个号打了4次红队，其中3次都喜提11点，这让我不禁。。想计算一下位于11点的概率究竟有多大

本帖仅考虑12人团，不考虑不到12人或者有人掉线的团(但是结果稍加变化即可用于不到12人的团)

此外，本帖只是算着玩儿，并没有什么实际的意义

首先，需要假设每个人翻牌结果独立同分布，即每个人翻牌的概率均相同，且相互独立、互不影响

其次，回顾一下普雷翻牌顺序的机制：

1.对于奖励不同者，按以下顺序排列：武器>首饰/特殊>传说卡>神器卡>账绑>24>13>12>11

2.对于奖励相同者，按照在团内的位置排列(红1-绿4)

第2点是导致“红队容易11点”的罪魁祸首

接下来是数学时间，不想看的可以直接跳过此段

对红1-绿4的12个角色分别编号1,2,...,12，记Ak="第k个角色翻到11点"，k=1,2,...,12

又记Bi="翻牌结果为第i种奖励"，i=1,2,...,N，N为总的翻牌结果数。设这些翻牌结果由差到好排列，即B1="翻到11个"，B2="翻到12个"，以此类推

显然所有的Bi构成一个完备事件组，因此由全概率公式可知 P(Ak)=∑P(Ak|Bi)P(Bi) (1)

考虑当i=2时的条件概率P(Ak|Bi)，即角色k在翻到12个的情况下位于11点，可想而知这个概率应该是非常低的，因为这要求全团都翻到≥12个，否则如果有人翻到11个，那么角色k就不是11点了

类似地考虑，当i更大时，P(Ak|Bi)会变得更小，因此可以(1)中忽略所有i≥2的求和项，认为 P(Ak)≈P(Ak|B1)P(B1)

对于P(Ak|B1)，即角色k在翻到11个的情况下位于11点，这要求之前的k-1个角色翻牌结果不能是11个，而之后12-k个角色的翻牌结果对此无影响

于是记P(B1)=p，则有P(Ak|B1)=(1-p)^(k-1)，从而P(Ak)≈p(1-p)^(k-1) (类似几何分布)

此时∑P(Ak)=1-(1-p)^12小于1，这很正常，因为我们直接在(1)式中截断了i≥2的项

如果想准确求出P(Ak)是多少，实际上思路和之前一致，这里直接给出结果：

经过mma暴力验证，对所有P(Ak)求和的确为1，所以结果应该没毛病

并且当N取1时，结果就是P(Ak)=p(1-p)^(k-1)

那么11点的概率究竟是多少呢?。。很可惜，由于官方没给出翻牌概率，我们虽然已经有了计算公式， 但是并没有办法得到具体结果，所以只能自己编数据了

利用近似结果P(Ak)=p(1-p)^(k-1)，其中翻到11个的概率p取0.3，则可得到：

这里所有概率加起来并不是100%，而是98.6%，是因为并没有考虑所有情况，但这个近似结果已经很令人满意了

如果要精确计算，则要给出所有翻牌奖励的概率，这里参考了网友的少量数据 ，取的概率为：

11个-30%，12个-25%，13个-25%，24个-7.5%，账绑-5%，粉卡-1.5%，传说卡-3%，首饰特殊-2.75%，界武器-0.25%

相应的概率长得跟之前几乎一模一样：

实际上，这个概率分布很大程度上依赖于翻到11个的概率，只有当翻到11个的概率比较小(显然不是)，或者人数较少时，才需要考虑后面的各项

如果分别取p=0.25和p=0.35，用近似公式得到的概率如下

总之，每个人位于11点的概率近似是一个首项为p，公比为1-p的等比数列。

红1在11点的概率约为翻到11个的概率p，之后每个人在11点的概率是前一个人的1-p倍。

但是，知道了位于11点的概率有多大，也改变不了你翻到金牌的概率，想要金牌还是得看脸。

不过更蛋疼的是，我们连11点的概率实际上也不知道，除非官方公布翻牌概率。。